Next: Quiz Up: Phase Equilibria Previous: Geometric Interpretation and Phase

Gibbs Phase Rule

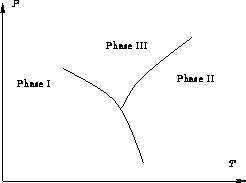
In each phase chemical potential $\mu$ is a function of P and T. Phase equilibrium condition:

$\begin{displaymath} \mu^{I}(P,T)=\mu^{II}(P,T)\end{displaymath}$

This determines a line in P-T plane. Two lines can intersect--there three phases meet! (Triple point).
$\begin{figure} \psfrag{P}{$P$} \psfrag{T}{$T$} \psfrag{Phase I}{Phase I} \ps... ...{Phase II} \psfrag{Phase III}{Phase III} \includegraphics{ternary}\end{figure}$
In other words, two equations

$\begin{displaymath} \left\{ \begin{aligned} \mu^{I}(P,T)&=\mu^{II}(P,T)\\ \mu^{I}(P,T)&=\mu^{III}(P,T) \end{aligned} \right.\end{displaymath}$

have one isolated solution!

Binary mixtures: we add a new variable--concentration c and have two chemical potentials $\mu_1$ and $\mu_2$ . What is the largest number of phases to coexist?

If there are r phases, we have r+2 variables (P, T, c^I, c^II,...). There are 2r chemical potentials--2(r-1) equations. They have unique solution, if r+2=2(r-1), or r=4. In binary solutions four phases can coexist in a special point!

General case: n-component mixture, r phases. We have 2+r(n-1) variables for n(r-1) equations. Maximal value for r is 2+r(n-1)=n(r-1), or

r=n+2

This is Gibbs Phase Rule. The maximum number of phases in equilibrium is two plus the number of components.