Subsections

• Problem
• Equation
• Solution
• Interpretation

Langevin Equation

Problem

We have one particle surrounded by small molecules. At t=0 it had $\mathbf{r}(0)=0$. We want to calculate its position at the time t.

Assumptions:

• The velocity $\mathbf{v}(t)$ is the slowest mode
• Friction coefficient is $\lambda m$

Equation

By definition,  

$$\frac{d\mathbf{r}}{dt} = \mathbf{v}$$ (1)

We already obtained equation for $d\mathbf{v}/dt$: 

$$\frac{d\mathbf{v}}{dt} = -\lambda\mathbf{v}+\mathbf{f}(t)$$ (2)

with random force $\mathbf{f}(t)$: 

$$\left\langle \mathbf{f}(t)\right\rangle=0,\quad \left\lang... ...f{f}(0)\mathbf{f}(t)\right\rangle=\frac{6kT\lambda}{m}\delta(t)$$ (3)

This is called Langevin equation. Langevin equation describes system with white noise acting on $\mathbf{v}$.

Solution

Let $\mathbf{v}(0)=\mathbf{v}_0$. In equilibrium  

$$\left\langle \mathbf{v}\right\rangle=0,\quad \left\langle \mathbf{v}_0^2\right\rangle=\frac{3kT}{m}$$ (4)

Solution of Langevin equation for $\mathbf{v}$ is  

$$\mathbf{v}(t) = \mathbf{v}_0e^{-\lambda t} + e^{-\lambda t}\int_0^t \mathbf{f}(\tau)e^{\lambda\tau}\,d\tau$$ (5)

Solution for $\mathbf{r}$ is

$$\mathbf{r}(t) = \int_0^t \mathbf{v}(\tau)\,d\tau$$

1.

Integration of the first term in (5):

$$\int_0^t \mathbf{v}_0e^{-\lambda\tau}\,d\tau = \frac{1}{\lambda}\mathbf{v}_0(1-e^{-\lambda t})$$

2.

Second term--by parts:

$$\begin{split} &\int_0^t\left[e^{-\lambda\tau}\int_0^\tau \... ...\lambda(\tau-t)}\right)\mathbf{f}(\tau)\, d\tau \end{split}$$

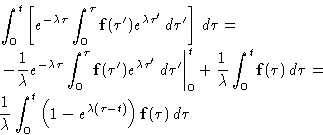
We obtained:

$$\mathbf{r}(t) = \frac{1}{\lambda}\mathbf{v}_0(1-e^{-\lambda ... ...0^t \left(1-e^{\lambda(\tau-t)}\right)\mathbf{f}(\tau)\,d\tau$$

Averages: we know $\left\langle \mathbf{v}_0^2\right\rangle$ and $\left\langle \mathbf{f}(0)\mathbf{f}(t)\right\rangle$. The cross-average

$$\left\langle \mathbf{v}_0\mathbf{f}(t)\right\rangle=0$$

1.

First term gives

$$\frac{1}{\lambda^2}(1-e^{-\lambda t})^2\left\langle \mathbf{v}_0^2\right\rangle=\frac{3kT}{m\lambda^2}(1-e^{-\lambda t})^2$$

2.

Second term gives

$$\begin{split} &\frac{1}{\lambda^2}\int_0^t d\tau \int_0^t d... ... \frac{1}{2\lambda}e^{-2\lambda t}-\frac32\right] \end{split}$$

Interpretation

We obtained:  

$$\begin{split} &\left\langle \mathbf{r}^2(t)\right\rangle =... ... \frac{1}{2\lambda}e^{-2\lambda t}-\frac32\right] \end{split}$$ (6)

At small times

$$\left\langle \mathbf{r}^2(t)\right\rangle = \frac{3kT}{m}t^2$$

At large t

$$\left\langle \mathbf{r}^2(t)\right\rangle = 6Dt,\quad D = \frac{kT}{m\lambda}$$

The large time limit could be obtained from the Wiener equation  

$$\frac{d\mathbf{r}}{dt}=\mathbf{g}(t)$$ (7)

with white noise $\mathbf{g}$:

$$\left\langle \mathbf{g}(t)\right\rangle=0,\quad \left\langle \mathbf{g}(0)\mathbf{g}(t)\right\rangle=12D\delta(t)$$

In the limit of small t Wiener equation does not work!

White noise in Wiener equation is the consequence of the averaging out a fast process--in our case, velocity relaxation!