Next: Quiz Up: Microscopic and Macroscopic States. Previous: Macroscopic State
![]()
![]()
![]()
Next: Quiz
Up: Microscopic and Macroscopic States.
Previous: Macroscopic State
Trajectory--a line in phase space. Many-body systems: a complex entangled trajectory. Assumption: after long time the system ``forgets'' the initial conditions. Probability of each state does not depend on where we started!
What can it depend upon? Energy, total momentum, total volume,...
| |
(1) |
| |
(2) |
| |
(3) |
Ergodicity hypothesis: ensemble average is equal to time average.
![]()
Is ergodic hypothesis alway correct?
Gibbs postulate: yes.
But how large should be ![]() in (1) for the
limit to work? What happens if it is a year? Twenty years? The
mountains flowed down at Thy presence
in (1) for the
limit to work? What happens if it is a year? Twenty years? The
mountains flowed down at Thy presence ![]() , but we are mortals....
, but we are mortals....
Examples: water is liquid at frequencies ![]() , but
solid at
, but
solid at ![]() . Window panes flow in hundred years...
. Window panes flow in hundred years...
Computer simulations: is the simulated system ergodic? Do we study its equilibrium or transient features?
Each system in the ensemble is a point in the phase space. How many points are there?
Answer:
![]()
![]()
Geometric interpretation: cell model
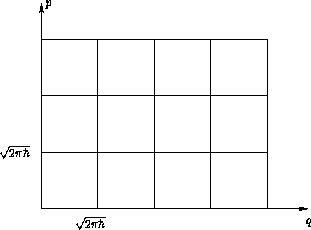
Entropy:
| |
(4) |
Suppose we increase the volume of our system V and the number of particles N.
![]()
![]()
Entropy of two non-interacting subsystems:
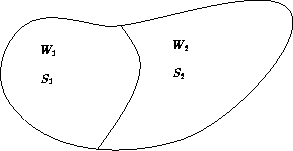
The total number of states:
![]()
S = S1 + S2
Thermodynamic limit: many weakly interacting parts!
Let ![]() be the probability to meet the given state in the
ensemble. Ensemble averaging:
be the probability to meet the given state in the
ensemble. Ensemble averaging:
![]()
| |
(5) |
![]()
© 1997 Boris Veytsman and Michael Kotelyanskii