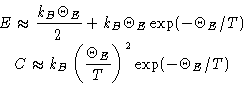Next: Einstein Model of Crystals
Up: Solid State
Previous: Equipartition Theorem
Subsections
Classical description: energy might have any value. One degree of
freedom--average energy kBT.
Quantum description: only portions of 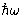 , with
, with
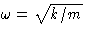 are allowed! Energy:
are allowed! Energy:
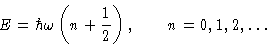
We say that the system has n phonons.
System might have as many phonons, as it wants (Bose-Einstein
statistics).![[*]](/icons/foot_motif.gif)
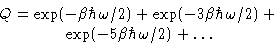
Geometric progression:
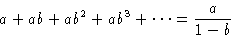
We have:
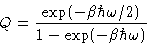
- Einstein Temperature:
- Let
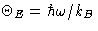 . Then
. Then
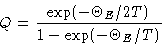
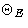 is Einstein temperature.
is Einstein temperature.
Free energy:
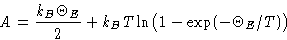
Entropy:
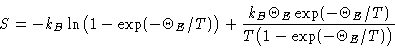
Energy:
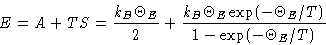
Heat capacity:
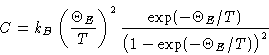
If
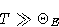
we obtain
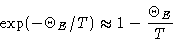
Then energy and heat capacity are
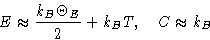
This is exactly classical result!
If
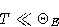
we obtain
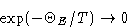
Energy and heat capacity:
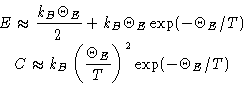
The vibrations are ``frozen'' at low temperatures!
© 1997
Boris Veytsman
and Michael Kotelyanskii
Wed Oct 1 00:45:35 EDT 1997
![]()
![]()
![]()
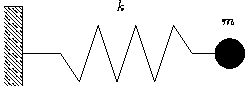
![]() , with
, with
![]() are allowed! Energy:
are allowed! Energy:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
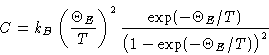
![]()
![]()
![]()
![]()
![]()